A Better Way to Divide the Pie 

I live and work in New Haven, Connecticut. Alongside Yale University, New Haven is famous for its pizza. Some are fiercely loyal to Sally’s and others to Pepe’s. Based on their long lines, you might think they are harder to get into than Yale. That’s because their clam pizzas are in a league of their own. At the risk of choosing sides, I look at a negotiation over a pie from Pepe’s.

Pepe’s will give Alice and Bob one of their 12-slice clam pizzas if they can agree on how to divide it up. If they can’t agree, Pepe’s will still give them half a pie, but with some favoritism: four slices will go to Alice and two to Bob.

There’s plenty of incentive to reach a deal. The challenge is there are many deals that work for both sides, some more favorable to Alice and others to Bob. They need to pick one. Most people employ one of two perspectives for how Alice and Bob might negotiate an agreement.

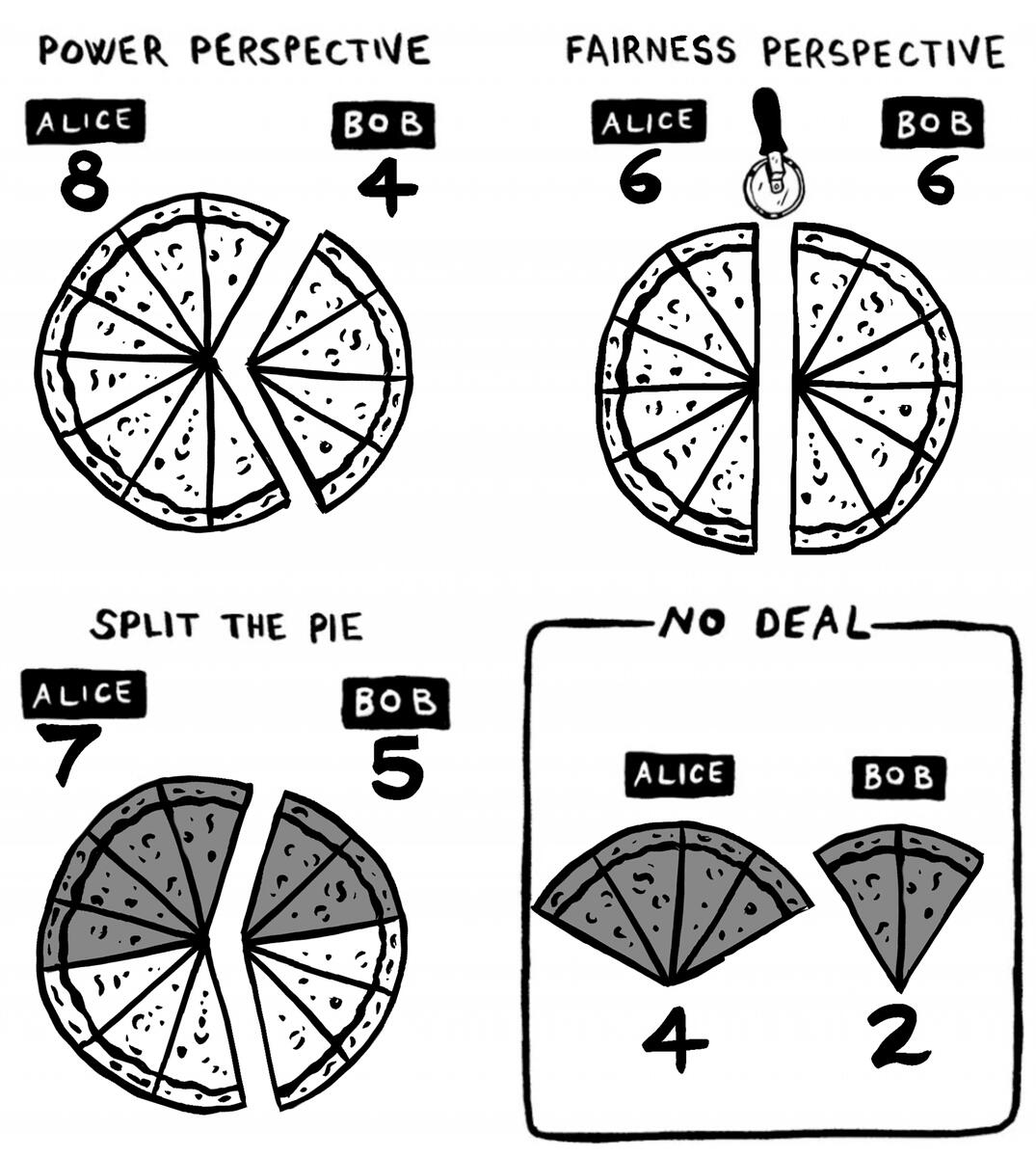
The first is the power perspective. Alice starts with more power—her fallback of 4 slices is twice as good as Bob’s—so she should get twice as much: 8 slices for Alice and 4 for Bob.

The second is the fairness perspective. The two sides focus on what each ends up with. In this scenario, they divide the pizza in half: Alice gets 6 slices and Bob gets 6 slices.

There is a different—and more logical—way to divide the pizza. It’s more logical because it focuses on what the negotiation is really about: the extra 6 slices created by an agreement. If Alice and Bob don’t reach a deal, they will have a total of 4 + 2 = 6 slices. If they reach a deal, they will have a total of 12 slices. The value of reaching a deal is to go from 6 to 12 slices. That increase of 6 slices is what’s at stake or what I call the negotiation pie. To get those 6 slices, Alice and Bob are equally needed. Because they have equal power, the 6 slices should be split equally. In addition, each side gets their fallback. This leads to an overall division of 4 + 3 = 7 slices to Alice and 2 + 3 = 5 slices to Bob.

While it seems odd to say this, most people end up being confused over what their negotiation is really about. They argue over the 12 slices, not the 6 slices. They focus on the whole pizza pie, not the relevant negotiation pie. The negotiation pie feels like an obvious idea hiding in plain sight. Once you frame the negotiation in terms of the relevant pie, the logical conclusion is that the relevant part of the pie should be divided evenly. That’s what I need to convince you of. And then I’m going to give you tools to convince others.

As a first step, I want to explain what’s wrong with the status quo. In my view, the power perspective confuses power outside the negotiation with power inside the negotiation. Why should the total amount be divided up in proportion to the fallback options? The slices are not negotiating with each other—Alice and Bob are. While 8:4 seems like a reasonable outcome because it mimics the ratio of their respective fallbacks, there is no inherent reason why the outcome should be based on such ratios.

Some might argue that Bob is in a weaker bargaining position since he will get just 2 slices if there’s no deal, while Alice will get 4 slices. That argument misses the point of the negotiation. If they don’t reach a deal, Alice will get nothing more than her 4 slices just as Bob will get nothing more than his 2. Effective negotiation is about beating your fallback. For Alice and Bob to beat their fallback, they are equally needed and hence equally powerful.

The second approach, an equal split of the total, is an oversimplified view of fairness. When it comes to dividing the 12 slices, Alice and Bob are not in equal positions. Alice has a better fallback. If 6:6 is really a viable view of fairness, it should work for any set of fallbacks. It doesn’t. Look what happens if Alice’s fallback option rises to 7 slices, while Bob’s stays fixed at 2 slices. In theory, the division should remain at 6:6. That is not going to happen. Alice would rather reject the deal—which gives her 7 slices—than accept 6 slices. While this flaw in an even split may not be apparent when the fallbacks are 4 and 2 slices, we see that as a rule for fairness, splitting the total in two is fundamentally flawed.

Splitting the total is a common mistake. Let’s say we assign the fallbacks at random and then have people do the negotiation. What do you predict? Just such an experiment was done by Nejat Anbarci and Nick Feltovich. Provided both fallbacks were no more than 6 slices, the two sides divided the total in half 42% of the time. It sounds fair and neither side does better by walking away. But as soon as one of the fallbacks was 7 or more slices, equal division was chosen less than 8% of the time.

What is going on is the two parties were grasping for a solution that looks fair. The problem is they haven’t learned to see the relevant pie as 12–(4 + 2) = 6 slices and so they end up splitting the wrong total. They split the 12 slices, not the 6 slices. It is fine to care about fairness, but fairness has to be applied to the relevant negotiation pie, not to the total. When it comes to the 6 slices, Alice and Bob are perfectly symmetric, equally positioned, and equally necessary. Dividing the negotiation pie equally is what’s fair.

Under the pie perspective, the negotiation pie of 6 is split 3 and 3. Each side gets their fallback plus half the pie. Alice ends up with 4 + 3 = 7 slices, and Bob gets 2 + 3 = 5 slices.

Splitting the negotiation pie is not just about fairness. Alice and Bob have equal power. If Alice doesn’t agree to the split, the negotiation pie is lost. The same is equally true for Bob. Neither party can be said to contribute more than the other to creating the negotiation pie of 6. Inside the negotiation, where the object is to create incremental value beyond where the parties are starting, the two parties are entirely symmetric. The two do have differential power outside the negotiation as reflected in their unequal fallbacks. But that has no bearing on how to divide up the negotiation pie.

Now you’ve seen the secret sauce. It may look deceptively simple in the pizza case, at least in hindsight. When we apply this approach to more complicated real-world problems, the pizza example underlies everything we do.